Log-Structured Merge-Tree
LSM 树 是针对写入性能优化的文件组织格式,通过避免离散地就地更新,实现比 B+ 树更高地写入吞吐。
背景
ACM 报告表明 [3]:
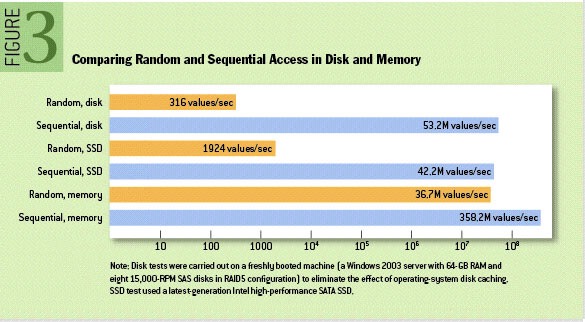
- 顺序硬盘 I/O 操作比随机内存访问更快
- 顺序硬盘 I/O 操作比随机硬盘 I/O 操作快了 3 个数量级,无论硬盘是固态硬盘还是机械硬盘
因此,对于频繁写入的系统,只对数据文件进行 append 操作(这种数据文件称为 logging、journaling 或者 heap file),几乎能达到磁盘写入速度上限。
日志文件虽然插入性能很好,但造成了 读放大:
- 当需要更新、删除某个值时,同时存在多个副本
- 当随机查找某个值时,需要逆时间顺序遍历所有文件直到找到
这导致纯 LSM 数 只能用于简单的场景,要么数据是完整访问的,比如 数据库 的 预写日志;要么是通过 offset 访问的,比如 Kafka 的消息队列。
初步设想
为了让日志文件支持更复杂的查询场景,比如点查询或范围查询,有四种优化方案:
- Search Sorted File:日志文件根据键值排序
- Hash:将数据分 bucket 存储
- B+ tree:使用索引文件结构比如 B+ 数、ISAM 等
- External file:额外创建一个哈希/索引文件
这几种方法都会造成写入性能降低,因为:
- 每次写入需要两次 I/O:读取页面、回写页面
- 每次写入需要更新数据结构:更新哈希/B+ 数索引,这又重新引入了就地更新操作,导致随机 I/O
为了解决这两个问题,通常解决办法是采用第四种 External file 方案,但是将索引保存在内存中。这个方案存在扩展性限制,比如当数据较小时,索引可能比数据还大。但该方案还是成功推广开来,比如 Riak、Oracle Coherence。
LSM 树
LSM 树 使用了完全不同的策略,保证日志文件写入性能的同时,加快了查询性能(虽然也比 B+ 树慢)。
- 当插入数据时,先写入内存缓冲(Mem Table),内存中的缓冲区用平衡树(比如红黑树)来维护键值顺序(该索引通常以 预写日志 方式在硬盘中维护一份副本)。当内存中的排序数据满了,就将整块数据写入硬盘新文件中,文件叫为 SST(Sorted String Table)。
- 后台进程定期执行 压缩(compaction)。压缩是将多个文件合并的过程,删除重复的数据、真正删除的数据,并将其余数据重新排序。由于原本各个文件都是有序的,因此这个排序非常高效。定期的压缩不仅删除了重复的数据,还减少了文件数量,以降低查询时需要查看的文件数。
- 当读取数据时,首先查看内存中的缓冲区。之后再倒叙查看所有文件,直到找到文件。由于文件是有序的,因此查找非常高效。但随着文件数量增加查找性能也会变差。为了加速查询,通常在内存中维护各个页面索引(page-index);为了减少文件查看,通常引入 布隆过滤器 以减少查看的文件。
事实上,LSM 树 就是将写入时的随机 I/O 变成了读取时的随机 I/O,这种交换在 OLAP 的场景是明智的。
In a nutshell LSM trees are designed to provide better write throughput than traditional B+ tree or ISAM approaches. They do this by removing the need to perform dispersed, update-in-place operations.[4]
On typical server hardware today, completely random memory access on a range much larger than cache size can be an order of magnitude or more slower than purely sequential access, but completely random disk access can be five orders of magnitude slower than sequential access. Even state-of-the-art solid-state (flash) disks, although they have much lower seek latency than magnetic disks, can differ in speed by roughly four orders of magnitude between random and sequential access patterns.[5]
So we need more than just a journal to efficiently perform more complex read workloads like key based access or a range search. Broadly speaking there are four approaches that can help us here: binary search, hash, B+ or external.
- Search Sorted File: save data to a file, sorted by key. If data has defined widths use Binary search. If not use a page index + scan.
- Hash: split the data into buckets using a hash function, which can later be used to direct reads.
- B+: use navigable file organisation such as a B+ tree, ISAM etc.
- External file: leave the data as a log/heap and create a separate hash or tree index into it.
One common solution is to use approach (4) A index into a journal – but keep the index in memory. So, for example, a Hash Table can be used to map keys to the position (offset) of the latest value in a journal file (log). This approach actually works pretty well as it compartmentalises random IO to something relatively small: the key-to-offset mapping, held in memory. Looking up a value is then only a single IO.[4:1]
O’Neil, Patrick, Edward Cheng, Dieter Gawlick, and Elizabeth O’Neil. “The Log-Structured Merge-Tree (LSM-Tree).” Acta Informatica 33, no. 4 (June 1996): 351–85. https://doi.org/10.1007/s002360050048. ↩︎
Chang, Fay, Jeffrey Dean, Sanjay Ghemawat, Wilson C. Hsieh, Deborah A. Wallach, Mike Burrows, Tushar Chandra, Andrew Fikes, and Robert E. Gruber. “Bigtable: A Distributed Storage System for Structured Data.” ACM Transactions on Computer Systems 26, no. 2 (June 2008): 1–26. https://doi.org/10.1145/1365815.1365816. ↩︎
http://www.benstopford.com/2015/02/14/log-structured-merge-trees/ ↩︎ ↩︎